2875. Changing
on a Segment (High)
n integers a0, a1,
..., an-1 are
given. Initially they all are 0. Then you have a list of queries to change some
elements or to print one element. The change query contains three integers l, r,
d. You must add to each element ai (l ≤ i ≤ r) the value d. The print query contains one integer i. You must print the current value ai.
Input. The first line contains two integers n and m – the number of elements and the number of queries. In the next m lines the queries are given. The change
query is given with the line "A l r
d", the print query is given with the line "Q i".
All values are integers, 1 ≤ n ≤ 106, 0 ≤ m ≤ 106, 0 ≤ l ≤ r < n, 0 ≤ i < n, |d| ≤ 103.
Output. For each print query output in a separate
line the current value of corresponding element.
Sample
input
10 6
A 3 7
1
Q 4
A 1 5
2
Q 4
Q 1
Q 6
Sample
output
1
3
2
1
SOLUTION
data structures – дерево Фенвика
Анализ
алгоритма
Задачу можно решить при помощи дерева
отрезков. Однако из-за ограничения n
≤ 106 решение не пройдет по памяти. Вместо поддержки функции
на отрезке (суммы, минимума) в задаче требуется выводить текущее значение
одного элемента. Поэтому воспользуемся деревом Фенвика, которое поддерживает
две функции:
1. Нахождение суммы на любом отрезке [L; R]
за время O(log2n);
2. Изменение значения любого элемента
массива за O(log2n);
При этом дерево требует O(n) памяти: именно столько, сколько
необходимо для хранения массива из n
элементов;
Заведем массив b целых чисел b0,
b1, ..., bn-1, изначально
равных нулю. При запросе на изменение (поступлении на вход тройки l, r,
d, в результате чего следует
выполнить операцию a[l..r]
+= d) будем делать следующие
изменения: bl увеличим на d, а br+1
уменьшим на d. Тогда при запросе на
вывод элемент ai равен
сумме b0 + b1 + ... + bi. Например, если l ≤ r < i, то изменения в
массиве b при операции a[l..r] += d никак не повлияют на значение ai.
Пример
Промоделируем работу запросов, приведенных
в примере.
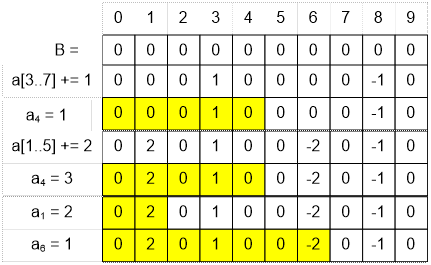
Реализация алгоритма
Дерево Фенвика храним в массиве Fenwick.
#define MAX 1000001
int Fenwick[MAX];
Функция
Summa0_i возвращает сумму элементов b0
+ b1 + ... + bi.
int Summa0_i(int i)
{
int result = 0;
for (; i >= 0; i = (i & (i + 1)) - 1)
result += Fenwick[i];
return result;
}
Изменение элемента: bi = bi + delta.
void IncElement(int i, int delta)
{
for (; i < n; i = (i | (i+1)))
Fenwick[i] += delta;
}
Основная
часть программы. Моделируем выполнение запросов.
scanf("%d
%d\n",&n,&m);
for(j = 0; j < m; j++)
{
scanf("%c",&command);
if (command == 'A')
{
scanf("%d %d %d\n",&l,&r,&d);
IncElement(l,d); IncElement(r+1,-d);
} else
{
scanf("%d\n",&i);
printf("%d\n",Summma0_i(i));
}
}